Find The Stable Vector Of
Get the answer to your homework problem.
Try Numerade free for vii days
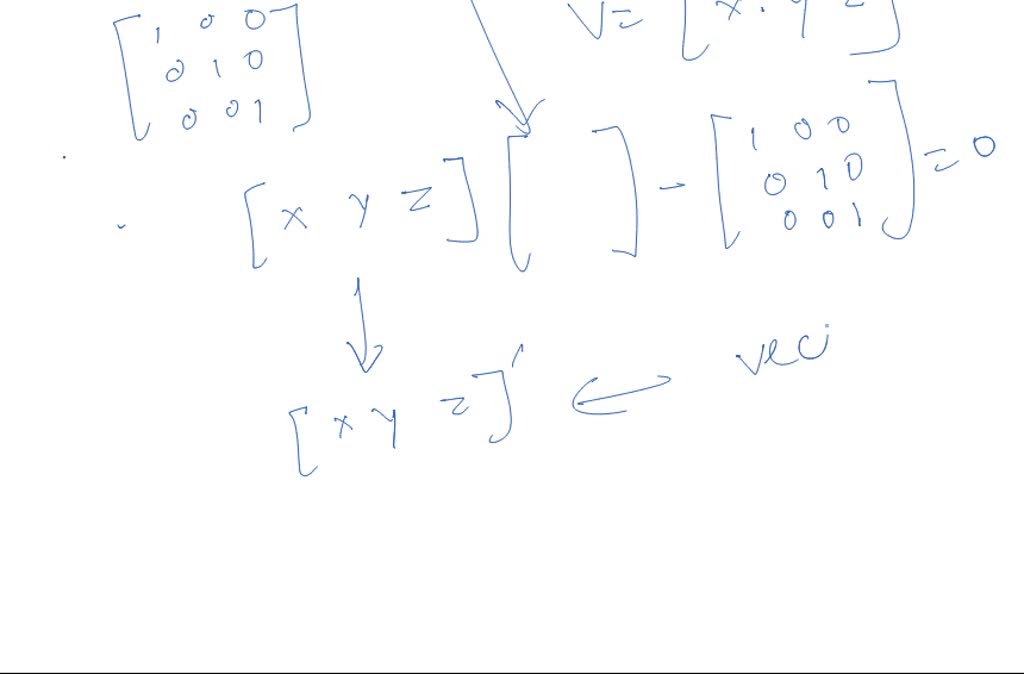
(1 point) Find the vector of stable probabilities for the Markov chain whose transition matrix is 0.six 0.2 0.ii 0.1 0.7 0.2 0.3 0.2 0.5
Related Question
betoken) Notice the vector of stable probabilities for the Markoff chain whose transition matrix is 0.5 0.v 0.6 0.4 0.three 0.vii W = xv/fifty 15/l fifteen/50
Discussion
You must be signed in to discuss.
Video Transcript
high in the given trouble, nosotros are required to find the vector which has the stable probability. Now the given transition matrix is ah nix 0.5, 0.5, 0.6, 0 0.iv, 0.iii, and zero. And so that's the transition matrix. Now we have ah the The Transition Matrix P. and Identity Matrix as i. So here we say that if we have this identity Matic 100 010 001. And let's say we accept a vector V. Is equal to Ten. Y. And said. Then when nosotros are multiplying X, Y. Z. With this transition vector. So 10. Y. And said with this given transition vector here ah And then we decrease the identity matrix. We will be getting this as equal zito considering as per the transition matrix holding and then the metrics that we will exist obtaining hither would be the the stable metric. And so here, when we transpose this, and then 10, Y and zed. When we transpose this, this is the the required ah vector of stable probabilities. Then this is the vector of stable probabilities. Nosotros are just required to discover the value of X, Y and Z. So here actually have been having three equations from the given ah condition. So the kickoff question is that minus X plus considering when we multiply x, Y. Z with the transition matrix will be getting that at aught. So from there we become minus Ten plus 0.65 Plus 0.iii, Z is equal to zero. And so this is equation one. Then the adjacent situation is 0.v x minus five plus 0.7 said is equal to nix. And this is equation as well. Side by side adjacent we have the question this 0.5 x plus nada bespeak for why minus said 2 0. And this is equation iii and also it is given that 10 plus Y plus Ten plus Y plus Z is equal to naught. And this is let's say this equation for. So now from all these 3 equations, four equation nosotros'll be getting the value of X. S X is equal to 0.34, and so Why is equal to 0.44 And Z is equal to 0.22. Hence the required matrix would exist of the task force course. And so this is 0.34, 0.44. 0.22. So this is the required metrics in the vector form. So that's the complete solution. Thank you.
Find The Stable Vector Of,
Source: https://www.numerade.com/ask/question/1-point-find-the-vector-of-stable-probabilities-for-the-markov-chain-whose-transition-matrix-is-06-02-02-01-07-02-03-02-05-89025/
Posted by: abelalowely1959.blogspot.com
0 Response to "Find The Stable Vector Of"
Post a Comment